概念

莱文斯坦距离(Levenshtein distance)是编辑距离的一种。它由俄罗斯科学家 弗拉基米尔·莱文斯坦在1965年提出。

两个字符串之间的莱文斯坦距离是将一个单词更改为另一个单词所需的最少编辑操作次数。莱文斯坦距离允许的编辑操作包括单个字符的 替换/插入/删除。

示例

“Saturday” 和 “Sundays” 之间的 Levenshtein 距离是 4

1.)  Saturday → Sturday  // 删除第一个 a
2.)  Sturday  → Surday   // 删除第一个 t
3.)  Surday   → Sunday   // 替换 r 为 n
4.)  Sunday   → Sundays  // 结尾添加 s

实现

莱文斯坦距离(Levenshtein distance)允许的编辑操作有三种，如果字符相等，我们还可以选择不操作。我们可以列举一下这四种操作的情况。

不操作

计算 "ay" 和 "day" 之间的莱文斯坦距离。

对于两个字符串的最后一位字符 “y”，我们可以选择不操作，也就是说， “ay” 和 “day” 之间的莱文斯坦距离等于 “a” 和 “da” 之间的莱文斯坦距离。

替换操作

计算 "dae" 和 "day" 之间的莱文斯坦距离。

对于两个字符串的最后一位字符 “e” 和 “y”，我们可以选择对最后一位字符进行替换操作，也就是说 “dae” 和 “day” 之间的莱文斯坦距离等于 “da” 和 “da” 之间的莱文斯坦距离加上 1。

插入操作

计算 "dae" 和 "da" 之间的莱文斯坦距离。

对于两个字符串的最后一位字符 “e” 和 “a”，我们可以选择在 “da” 后进行插入操作，也就是说 “dae” 和 “da” 之间的莱文斯坦距离等于 “da” 和 “da” 之间的莱文斯坦距离加上 1。

删除操作

计算 "dae" 和 "daey" 之间的莱文斯坦距离。

对于两个字符串的最后一位字符 “e” 和 “y”，我们可以选择在 “daey” 后进行删除操作，也就是说 “dae” 和 “daey” 之间的莱文斯坦距离等于 “dae” 和 “dae” 之间的莱文斯坦距离加上 1。

动态规划

从四种操作我们可以看出来，四种操作都可以被分解为多个重叠子问题。对于重叠子问题，我们一般会采用动态规划的方案。

通过 dp table 来更统计重叠子问题的莱文斯坦距离，当我们统计到 table 右下角时，就找到了 “Saturday” 和 “Sundays” 之间的莱文斯坦距离。

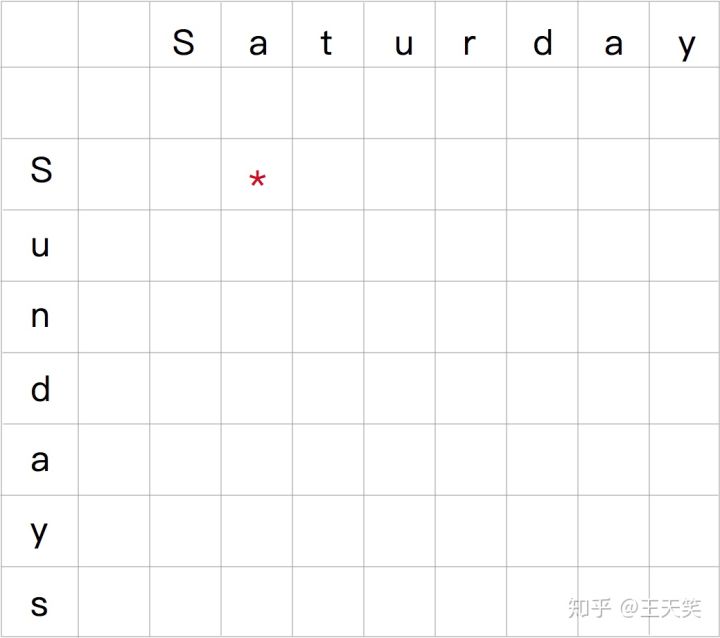
*的位置表示 Sa 和 S 子问题的莱文斯坦距离

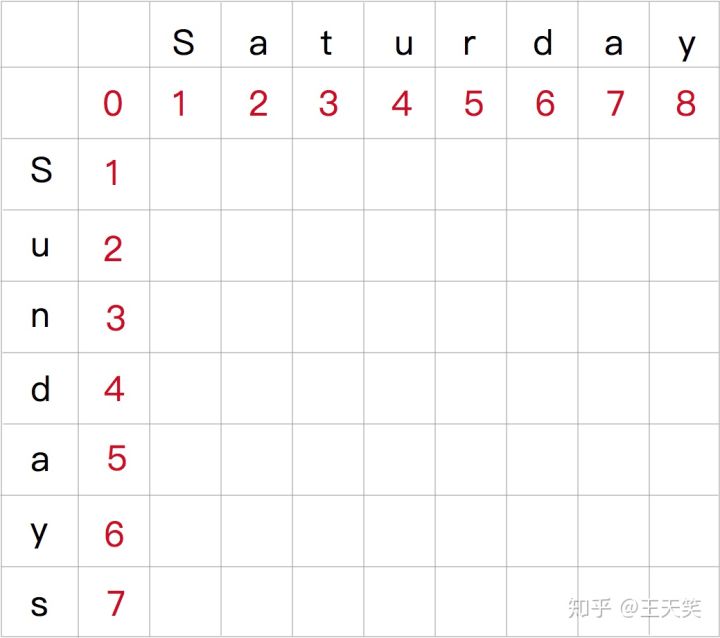
首先计算空字符串到 “Sundays” 各个重叠子问题的 莱文斯坦距离，我们只能进行插入操作。

空字符串和 Sundays 各个重叠子问题的 莱文斯坦距离

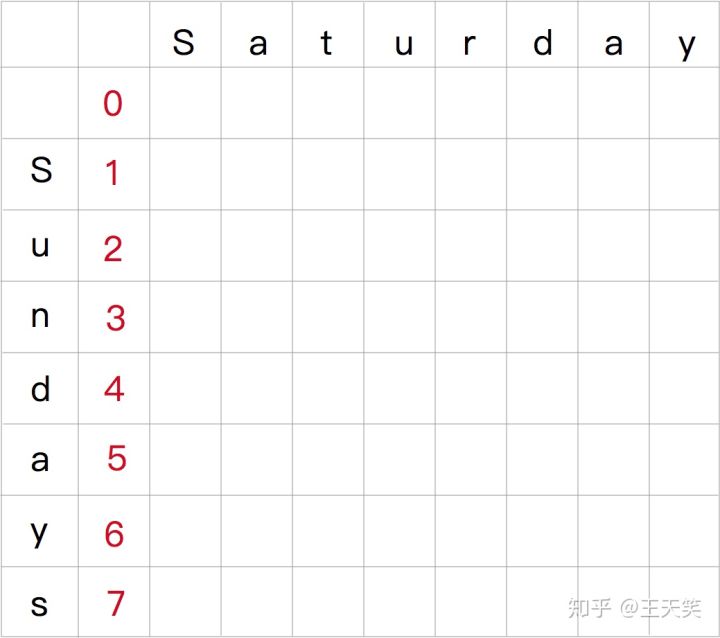
然后计算 “Saturday” 各个子串到 空字符串的莱文斯坦距离，我们只能进行删除操作。

Saturday 各个子串到 空字符串的莱文斯坦距离

做完这些初始化操作，我们就可以正式开始对比各个子串之间的莱文斯坦距离了。莱文斯坦距离的各个操作值都可以很容易的在 dp table 中查找到。

当字符相等时，不需要做任何操作。对应子串的莱文斯坦距离就等于前一个子串的莱文斯坦距离。

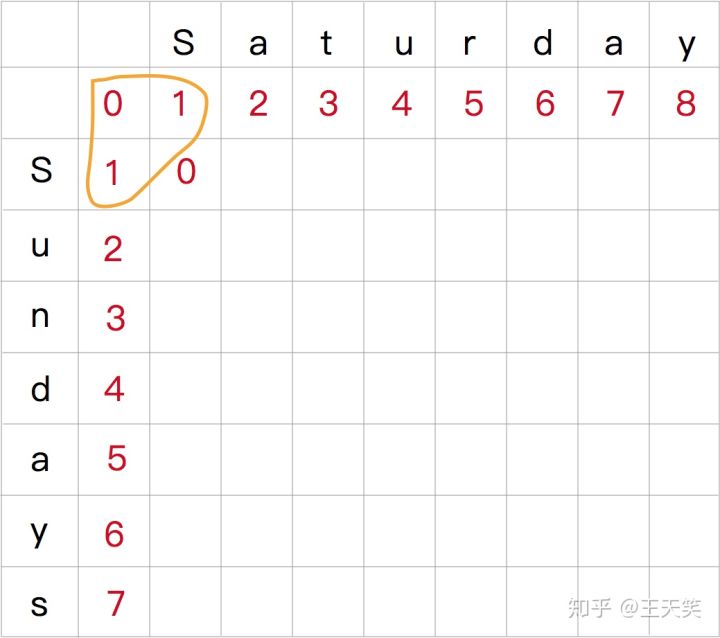
因为 S 与 S 相等，不需要做任何操作。对应子串的莱文斯坦距离就等于上一个子串 替换/插入/删除 后得到的最小值，也就是 Math.min(1,0,1)。

当字符串不相等时，我们可以做 替换/插入/删除 操作，这些操作都等于 上一个子串的莱文斯坦距离加一。

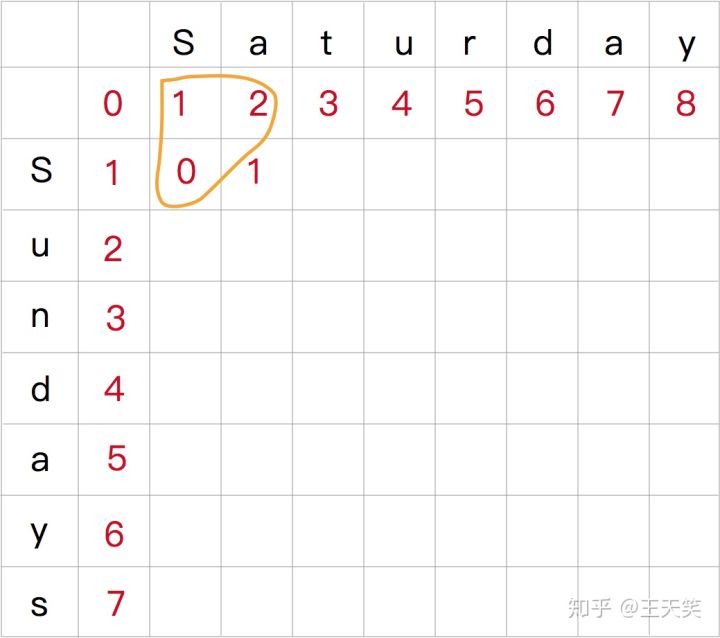
因为 S 与 a 不相等，需要做替换/插入/删除。对应子串的莱文斯坦距离就等于上一个子串 替换/插入/删除 后得到的最小值加上 1，也就是 Math.min(1,2,1) + 1。

不断重复这个步骤，直到求出 dp table 右下角的值，就是我们最终得到的 “Saturday” 和 “Sundays” 之间的莱文斯坦距离。

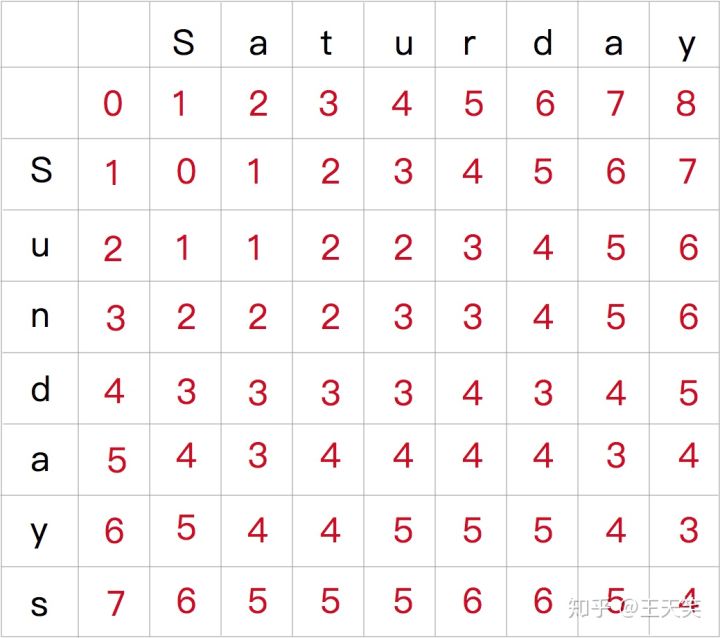
Saturday 和 Sundays 之间的莱文斯坦距离是 4

JavaScript 代码实现

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
var minDistance = function(word1, word2) {
  const dp = [];
  const m = word1.length;
  const n = word2.length;

  for (let i = 0; i < m + 1; i++) {
    const tmp = [];
    for (let j = 0; j < n + 1; j++) {
      if (i === 0) {
        tmp.push(j);
      } else if (j === 0) {
        tmp.push(i);
      } else {
        tmp.push(0);
      }
    }
    dp.push(tmp);
  }

  for (let i = 1; i < m + 1; i++) {
    for (let j = 1; j < n + 1; j++) {
      if (word1[i-1] === word2[j-1]) {
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;
      }
    }
  }
  return dp[m][n];
};

时间复杂度是 O(nm)

莱文斯坦距离的应用

• 拼写检查
• 语音辨识
• DNA分析
• 抄袭侦测

参考：

https://en.wikipedia.org/wiki/Levenshtein_distance https://www.youtube.com/watch?v=MiqoA-yF-0M&t=61s