xiaoyuhen's blog
About

背包问题（Knapsack-problem）详解

March 30, 2019

概念

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，如何选择最合适的物品放置在背包中才能使物品的价格最高。

背包问题

示例

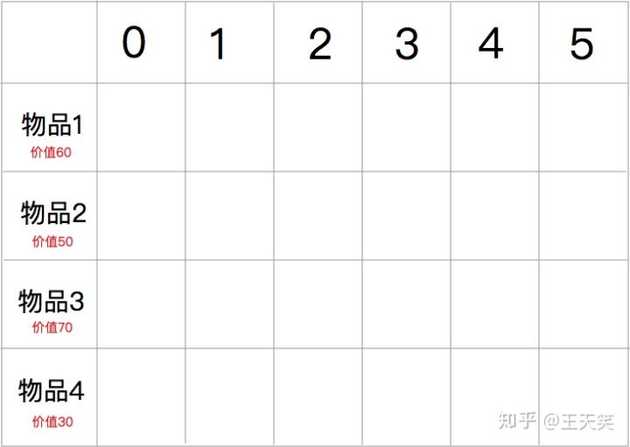
背包重量为 5

物品1：重量为 5，价格为 60
物品2：重量为 3，价格为 50
物品3：重量为 4，价格为 70
物品4：重量为 2，价格为 30

选择物品2+物品3能够使背包中的物品价格最高。

解法

我们可以很容易通过递归来解决这类组合问题。如果我们能从中找出重叠的子问题，就可以通过动态规划的方式来优化解法。

动态规划

对于物品x，我们都可以进行两个操作，选/不选。所有选/不选的操作都能转化成对应的重叠子问题，我们以物品4为例：

  • 选：问题转化为背包重量为 3，在物品1/2/3中设计选择方案使得物品的总价值最高的子问题。
  • 不选：问题转化为背包重量为 5，在物品1/2/3中设计选择方案使得物品的总价值最高的子问题。

比较选与不选哪个是最优解，一直重复类似步骤最后得到最终答案。

定义 dp table v2 9bed91f9104d9442ad6ed68112b677f6 hd

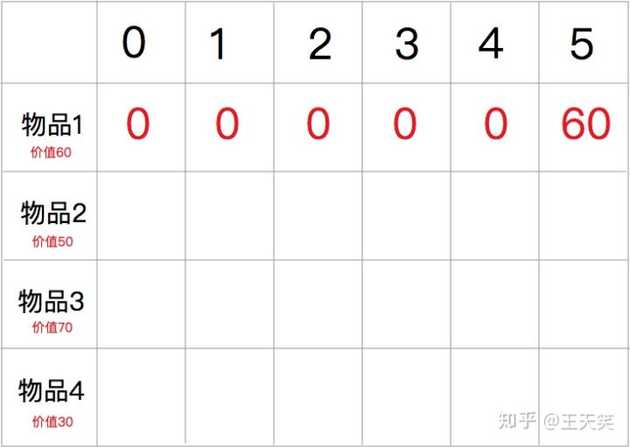
物品1的重量为 5，价值为 60，所以对于物品1，最合适的物品放置方案就是只放入一个物品1，我们得到的价格为 60。

只放入物品1 的价值为 60 v2 c0ef22f0855e58e3efd7452780e0f127 hd

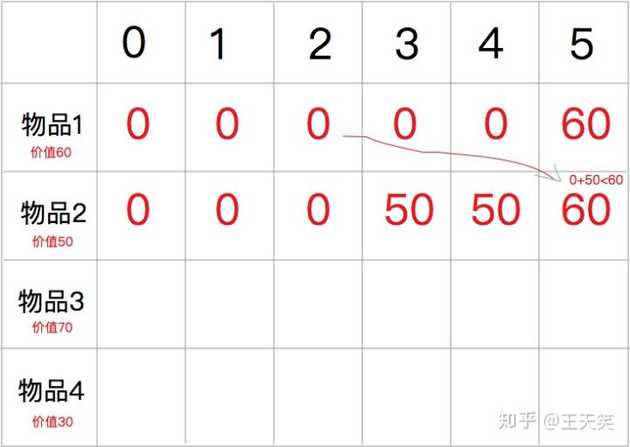
物品2的重量为3，价值为 50，对于物品1和物品2来说，我们可以放入一个物品1，也可以放入一个物品2，但需要选择出最高的价值。

只放入一个物品1价值为 60，只放入一个物品2价值为 50。两个物品放入的最优解是放入物品1。 v2 ef5f8e8019b1a86ac855800aa0944265 hd

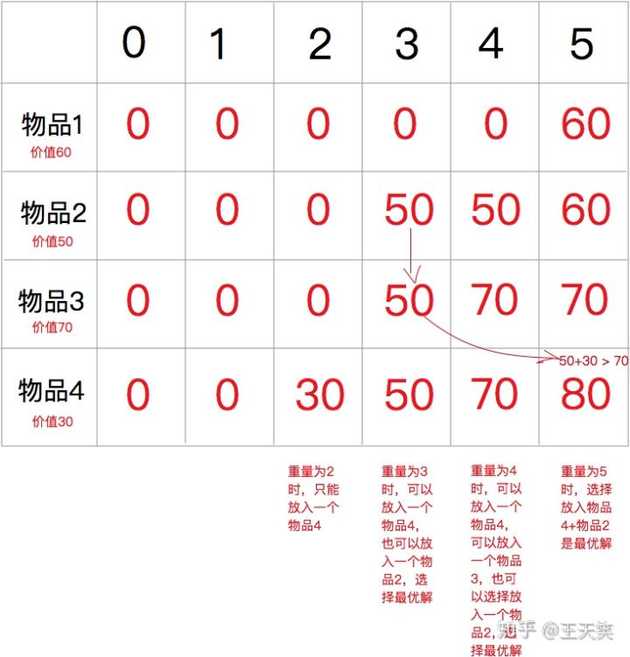
物品3重量为4，价值为70，对于物品3来说，我们可以放入一个物品1，也可以放入一个物品2，也可以放入一个物品3，但需要选择出最高的价值。

只放入一个物品1价值为 60，只放入一个物品2价值为 50，只放入一个物品3价值为 70。两个物品放入的最优解是放入物品3。 v2 4282efde84cdfee4ddd4cf9b60c90872 hd

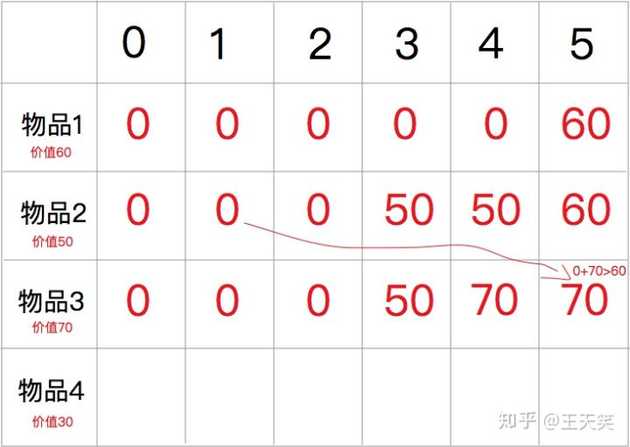
物品4重量为2，价值为 30，对于物品4来说，我们可以放入一个物品1，可以放入一个物品3，也可以放入一个物品3+一个物品4，但需要选择出最高的价值。

重量为5 时，选择放入物品4+物品2是最优解 v2 2bef29e35223576cbf25395ab29ca347 hd

JavaScript 示例代码

function knapsack(weights, values, W) {
  const n = weights.length;
  const dp = new Array(n + 1).fill().map(() => new Array(W + 1).fill(0));

  for (let i = 1; i < dp.length; i++) {
    for (let j = 0; j < dp[i].length; j++) {
      if (j - weights[i - 1] >= 0) {
        const value = values[i - 1] + (dp[i - 1][j - weights[i - 1]] || 0);
        dp[i][j] = Math.max(value, dp[i - 1][j]);
      } else {
        dp[i][j] = dp[i - 1][j] || 0;
      }
    }
  }

  return dp[weights.length][W];
}

时间复杂度 O(nm)，空间复杂度 O(nm)

优化空间

实际上，我们并不需要一个二维的 dp table 来存储对应的值，如果把重复的值进行合并，我们完全可以在一个一维 dp table 中进行存储。

如果是一个一维 dp table，我们只需要不断更新 2/3/4/5 的值就可以 v2 b5abd1e77539bd6255cb3f18ba59f8fb hd

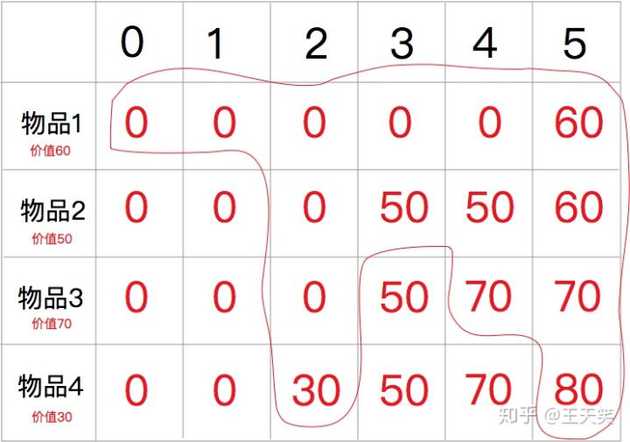
JavaScript 示例代码

function knapsack(weights, values, W) {
  const dp = new Array(W + 1).fill(0)

  for (let i = 0; i < weights.length; i++) {
    for (let j = 0; j < dp.length; j++) {
      if (j - weights[i] >= 0) {
        const value = values[i] + (dp[j - weights[i]] || 0)
        dp[j] = Math.max(value, dp[j]);
      }
    }
  }

  return dp[W];
}

时间复杂度 O(n*m)，空间复杂度 O(n)

类似问题

很多问题都可以转换为背包问题去求解。

分割等和子集(partition-equal-subset-sum)

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

如果数组的总和为奇数，则不可能分割为等和子集。如果数组的总和为偶数，则可以转换为重量为 22 / 2 = 11 的背包，数组中的值能否塞满背包的问题。

JavaScript 代码示例

/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canPartition = function(nums) {
  const num = nums.reduce((pre, cur) => pre + cur, 0);

  if (num % 2 !== 0) {
    return false;
  }

  const count = num / 2;

  const dp = new Array(count + 1).fill(false);
  dp[0] = true;
  for (let i = 0; i < nums.length; i++) {
    if (dp[count - nums[i]]) {
      return true;
    }
    for (let j = count; j >= nums[i]; j--) {
      dp[j] = dp[j - nums[i]];
    }
  }

  return false
};

零钱兑换2(Coin Change 2)

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

可以转化为完全背包问题，然后再把完全背包转化为普通背包问题。

JavaScript 代码示例

/**
 * @param {number} amount
 * @param {number[]} coins
 * @return {number}
 */
var change = function(amount, coins) {
  const dp = new Array(amount + 1).fill(0);
  dp[0] = 1;
  for (const coin of coins) {
    for (let i = coin; i <= amount; i++) {
      dp[i] += dp[i - coin];
    }
  }
  return dp[amount];
};

应用

背包问题（Knapsack problem）是一种组合优化的 NP 完全问题，相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。

参考

https://www.youtube.com/watch?v=DJ4a7cmjZY0 https://youtu.be/xCbYmUPvc2Q https://en.wikipedia.org/wiki/Knapsack_problem